三角函数值速查表

在数学的广阔天地里，三角函数无疑是一片璀璨星空，它们不仅在几何学中占据重要地位，更是物理、工程等多个领域不可或缺的工具。而在这星空中，有一张神奇的“地图”——三角函数值表，它就像一座桥梁，连接着理论与实践，让复杂的计算变得简单直观。今天，我们就来一起揭开三角函数值表的神秘面纱，看看它是如何帮助我们探索三角函数世界的奥秘。

初识三角函数

首先，让我们简单回顾一下三角函数的基本概念。三角函数，主要包括正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc），它们与直角三角形的边长和角度密切相关。正弦是对边与斜边之比，余弦是邻边与斜边之比，正切是对边与邻边之比，其余三个则是这三者的倒数关系。这些比例关系，随着角度的变化而变化，构成了三角函数的基本特性。

三角函数值表的诞生

在实际应用中，我们经常需要知道某个特定角度下的三角函数值。如果每次都通过构建直角三角形来计算，不仅效率低下，而且容易出错。于是，数学家们经过精心计算和验证，编制出了三角函数值表，这张表列出了从0°到360°（或0到2π弧度）之间，每隔一定角度（如1°、5°、15°等）的三角函数值。这样，我们只需查找表格，就能快速获取所需信息，大大提高了工作效率和准确性。

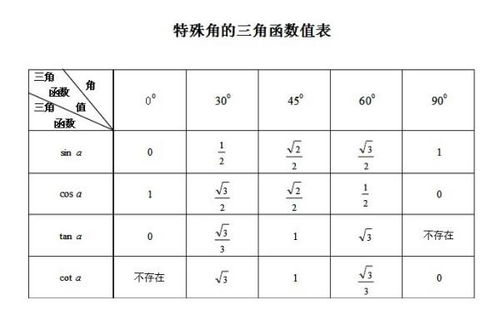
三角函数值表的结构

三角函数值表通常按照角度排列，从左到右依次列出正弦、余弦、正切等函数的值。以角度制为例，表格的第一列可能是角度值，如0°、1°、2°...直到360°；接下来的几列则分别对应这些角度下的sin、cos、tan等函数值。有些表格还会包括弧度制的角度表示，以及小数形式的函数值，以满足不同需求。

如何使用三角函数值表

使用三角函数值表非常直观。假设我们需要查找30°角的正弦值，首先找到表格中30°对应的行，然后查看该行“sin”列下的数值即可。如果表格中的角度不是以1°为单位，比如是5°为一个间隔，那么对于非整5°的角度，我们可能需要通过插值法来估算其值，但大多数情况下，对于常见角度，表中都会直接给出精确值。

三角函数值表的实用价值

三角函数值表在多个领域发挥着重要作用：

工程设计与建筑：在设计桥梁、建筑时，需要精确计算结构的角度和长度，三角函数值表提供了便捷的计算手段。

物理学：在力学、波动学等领域，三角函数是描述周期性现象（如振动、波动）的重要工具，值表帮助科学家快速获取关键数据。

天文学：在研究天体运行轨迹时，三角函数用于计算天体之间的角度关系，值表是天文学家不可或缺的参考资料。

电子与通信：在信号处理、波形生成等方面，三角函数值表有助于设计精确的信号波形和频率。

计算机图形学：在3D建模、动画制作中，三角函数用于计算物体的旋转、缩放等变换，值表是图形渲染的基础之一。

理解三角函数值的变化规律

通过观察三角函数值表，我们可以发现一些有趣的规律：

正弦函数（sin）：在0°到90°之间，随着角度的增加，sin值从0增加到1；在90°到180°之间，sin值逐渐减小至0；之后，在180°到270°之间为负值，且绝对值逐渐增大至1；270°到360°则又逐渐减小至0。整个周期中，sin函数呈现出一个完整的波形。

余弦函数（cos）：cos函数的变化趋势与sin相反，它在0°时达到最大值1，随着角度增加至90°，cos值逐渐减小至0；之后，在90°到270°之间保持负值，且在180°时达到最小值-1；270°到360°则逐渐回升至0。

正切函数（tan）：tan函数在每个象限内的变化趋势不同，但在0°、90°、180°和270°等特殊角度处未定义（因为分母为0）。在0°到90°之间，tan值从0开始逐渐增加；90°到180°为负值且逐渐减小；180°到270°为正值且逐渐增加；270°到360°则又逐渐减小至0。

数字化时代的三角函数值表

随着科技的发展，三角函数值表已经不仅仅局限于纸质形式。现代计算器、编程语言和在线工具都能快速计算任意角度的三角函数值，大大提高了计算的灵活性和