无理数的定义与解释

在数学的世界里，有一类数字既神秘又引人入胜，它们既不像整数那样直观明了，也不似有理数（即可以表示为两个整数之比的数）那样易于理解和操作，这类数字就是无理数。无理数的概念，从古希腊数学家毕达哥拉斯学派的一次意外发现开始，就一直是数学研究和哲学探讨的热点。那么，究竟什么是无理数？它们为何如此特别？又如何在日常生活中找到它们的踪迹呢？

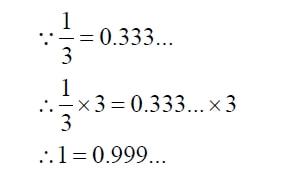
无理数的定义

首先，我们需要明确无理数的定义。简单来说，无理数是不能表示为两个整数之比的数，即它们不能写成a/b的形式（其中a和b是整数，且b不为0）。换句话说，无理数的小数部分是无限不循环的。这与有理数形成鲜明对比，有理数的小数部分要么是有限的，要么是无限循环的。

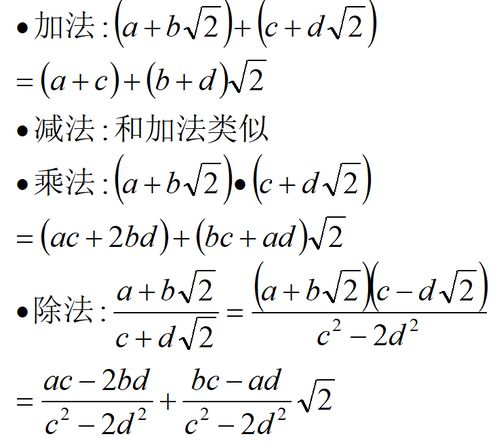
无理数的发现

无理数的发现，通常归功于古希腊数学家希帕索斯。他是毕达哥拉斯学派的一员，该学派坚信“万物皆数”，即世界上的一切都可以表示为整数或整数之比。然而，希帕索斯在研究正方形的对角线长度时，发现了一个令人震惊的事实：正方形的对角线与其边长之比，竟然是一个无法表示为两个整数之比的数。这一发现直接挑战了毕达哥拉斯学派的核心信念，据说希帕索斯因此被学派视为叛徒，甚至遭受了不幸的命运。

尽管希帕索斯的故事可能带有传奇色彩，但无理数的存在确实对当时的数学观念产生了巨大冲击。它迫使数学家们重新审视数的概念，并承认除了有理数之外，还存在另一种无法用简单比例表示的实数。

无理数的特性

无理数具有几个显著的特性，这些特性使它们在数学中占据独特地位：

1. 无限不循环小数：无理数的小数部分是无限不循环的，这意味着我们无法通过有限次计算或观察来精确确定其值。例如，π（圆周率）和e（自然对数的底数）都是著名的无理数，它们的小数部分既无限又不循环。

2. 不可约分：无理数不能表示为两个整数的比，这意味着它们在任何情况下都无法被简化为更简单的分数形式。这一特性使得无理数在有理数系中显得“格格不入”。

3. 密度性：在实数轴上，无理数与有理数一样密集分布。这意味着在任意两个有理数之间，都可以找到无数个无理数；同样，在任意两个无理数之间，也可以找到无数个有理数。这种密度性使得无理数在实数系中占据了不可忽视的地位。

无理数的应用

尽管无理数在数学上显得“另类”，但它们在现实生活中的应用却无处不在。以下是一些无理数应用的实例：

1. 几何学：在几何学中，无理数经常出现在与圆相关的计算中。例如，圆的周长与直径之比就是π，一个典型的无理数。同样地，正方形的对角线长度与其边长之比也是无理数（具体为√2）。这些无理数的出现，使得几何学中的许多计算变得复杂而有趣。

2. 物理学：在物理学中，无理数也扮演着重要角色。例如，在量子力学中，波函数的周期性往往与无理数有关；在热力学中，熵的计算也可能涉及无理数。此外，在描述自然现象的方程中，无理数也经常出现作为常数或参数。

3. 工程学：在工程学中，无理数的应用同样广泛。例如，在信号处理中，傅里叶变换的频域表示往往涉及无理数；在电路设计中，电容和电感等元件的阻抗计算也可能涉及无理数。这些无理数的出现，使得工程问题的解决变得更加精确和复杂。

4. 计算机科学：在计算机科学中，无理数的应用也不容忽视。例如，在计算几何中，处理圆的周长和面积时就需要用到π；在数值分析中，求解某些方程时也可能涉及无理数的近似计算。此外，在加密算法和随机数生成器中，无理数也发挥着重要作用。

无理数的挑战与争议

尽管无理数在数学和现实生活中有着广泛的应用，但它们也带来了一些挑战和争议。例如，由于无理数的小数部分是无限不循环的，我们无法通过有限次计算来精确确定其值。这在实际应用中可能会导致精度损失或计算困难。此外，无理数的存在也引发了关于数学基础的深刻思考：既然无理数无法用整数之比来表示，那么它们是否真的是“真实的”数？这个问题一直困扰着数学家和哲学家们。

然而，随着数学的发展，我们逐渐认识到无理数是实数系中不可或缺的一部分。它们不仅在数学理论中扮演着重要角色，还在实际应用中发挥着巨大作用。因此，尽管无理数可能带来一些挑战和争议，但它们仍然是数学和现实生活中不可或缺的元素。

结语

无理数作为数学中的一类特殊数字，既神秘又引人入胜。它们无法用简单的整数之比来表示，小数部分是无限不循环