如何轻松计算误差值

在数据处理与分析的广泛领域中，误差值的计算是至关重要的一环。它不仅关系到结果的准确性，还直接影响到决策的有效性和科学性。误差值，简而言之，是衡量观测值或计算值与真实值之间差异大小的量度。本文将从多个维度探讨误差值的计算方法，包括基本概念、常见类型、具体计算方法、实际应用中的注意事项以及误差减少策略，以期为相关领域的工作者和学习者提供全面的理解和指导。

一、误差值的基本概念

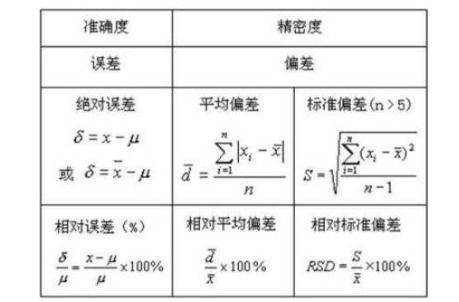
误差值，又称为误差，是观测值或实验值与公认的真实值或理论值之间的差异。在科学研究、工程应用、统计分析等领域，由于测量工具的不精确、环境因素的影响、人为操作的误差等多种原因，实际获得的数据往往与真实值存在偏差。这种偏差即为误差。

误差值可以分为绝对误差和相对误差两种基本形式。绝对误差是指观测值与真实值之间的差的绝对值，反映了误差的具体大小；相对误差则是绝对误差与真实值的比值，通常以百分比形式表示，用于比较不同量纲或数量级数据之间的误差水平。

二、误差值的常见类型

误差值根据来源和性质的不同，可以进一步细分为以下几种类型：

1. 系统误差：系统误差是由测量仪器、方法或环境条件等固定因素引起的，具有单向性和可重复性。例如，温度计长期使用后可能出现的读数偏高或偏低。

2. 随机误差：随机误差是由不可预测的随机因素引起的，如空气中的微小扰动、操作人员的微小抖动等。这类误差的特点是大小和方向均不固定，且符合统计规律。

3. 粗大误差：粗大误差通常是由于操作失误、记录错误或仪器故障等明显原因造成的异常值，也称为过失误差。这类误差可以通过数据审核和异常值检测等方法进行识别和剔除。

三、误差值的具体计算方法

1. 绝对误差的计算

绝对误差ΔE的计算公式为：

ΔE = |观测值 - 真实值|

例如，某次测量的实际长度为10.5cm，而真实长度为10.0cm，则绝对误差为：

ΔE = |10.5 - 10.0| = 0.5cm

2. 相对误差的计算

相对误差rE的计算公式为：

rE = (ΔE / 真实值) × 100%

继续上面的例子，相对误差为：

rE = (0.5 / 10.0) × 100% = 5%

3. 标准误差的计算

标准误差SE用于衡量样本均值与总体均值之间可能存在的误差，常用于统计分析中。其计算公式为：

SE = σ / √n

其中，σ为样本标准差，n为样本量。标准误差越小，说明样本均值越接近总体均值。

4. 均方误差MSE的计算

均方误差MSE是衡量预测值与实际值之间差异大小的常用指标，在回归分析、机器学习等领域广泛应用。其计算公式为：

MSE = Σ(观测值 - 预测值)^2 / n

MSE越小，表示模型的预测精度越高。

四、实际应用中的注意事项

1. 误差来源的识别与控制：在进行实验或测量前，应尽可能识别并控制可能的误差来源，如选择合适的测量工具、优化实验方法、改善环境条件等。

2. 误差值的合理评估：计算误差值时，应根据具体情况选择合适的误差类型（如绝对误差、相对误差）和计算方法。同时，要注意误差值的合理范围，避免过度解读或忽视误差。

3. 数据质量控制：对于采集到的数据，应进行严格的质量控制，包括数据审核、异常值检测、数据清洗等步骤，以确保数据的准确性和可靠性。

4. 误差的传递与累积：在复杂系统或过程中，误差可能会传递和累积，导致最终结果的不准确。因此，在设计和分析过程中，应充分考虑误差的传递效应，采取相应的措施进行修正和补偿。

五、误差减少策略

1. 提高测量精度：选用精度更高的测量仪器和方法，减少系统误差和随机误差的影响。

2. 多次测量取平均值：通过多次重复测量并取平均值，可以有效降低随机误差的影响，提高测量结果的准确性。

3. 数据校准与修正：对测量数据进行校准和修正，以消除或减小系统误差的影响。例如，对温度计进行定期校准，确保其读数准确。

4. 采用先进的数据处理技术：利用现代数据处理技术，如数据融合、滤波、插值等方法，对原始数据进行预处理和优化，提高数据的可靠性和准确性。

5. 加强人员培训与管理：提高操作人员的专业技能和责任心，减少人为操作误差的发生。同时，建立完善的质量管理体系，对实验过程和数据质量进行全程