双曲线有哪些重要的知识点？

探索双曲线的奥秘：一场数学世界的奇妙之旅

在数学的浩瀚宇宙中，双曲线如同一对优雅的舞者，以其独特的身姿和迷人的性质，吸引着无数数学爱好者的目光。它们不像圆或椭圆那样完美闭合，却以开放的姿态，向无限延伸，展现出一种不拘一格的美。今天，就让我们一同踏上这场探索双曲线知识点的奇妙之旅，揭开它神秘而迷人的面纱。

一、双曲线的定义：从直观到抽象的跨越

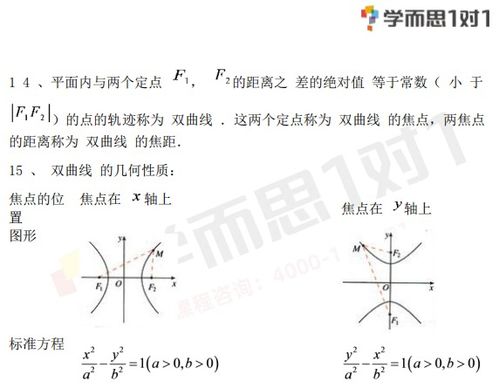
双曲线，这个名字本身就充满了诗意和想象空间。简单来说，双曲线是由平面上到两个定点（称为焦点）的距离之差的绝对值等于常数（且这个常数小于两焦点之间的距离）的点的轨迹形成的。想象一下，你站在一个空旷的操场上，手中拿着两根等长的绳子，分别系在两个固定的点上（焦点）。当你以特定的步伐（即上述的常数）移动，使两根绳子始终保持绷紧且长度之差不变时，你的足迹就会描绘出一条双曲线。

这个定义看似简单，却蕴含了深刻的数学原理。它揭示了双曲线与焦点、直线（称为渐近线）以及常数之间的紧密联系。而正是这种联系，让双曲线在数学、物理乃至天文学中都有着广泛的应用。

二、双曲线的标准方程：数与形的完美融合

要深入了解双曲线，离不开它的标准方程。对于中心在原点、焦点在x轴上的双曲线，其标准方程为：

\[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]

其中，a和b是常数，且a、b均大于0。这个方程看起来有些复杂，但当你把它与双曲线的几何图像结合起来时，就会发现它们之间的和谐之美。

在这个方程中，a代表双曲线与x轴交点到原点的距离（即实轴半径），而b则与双曲线的开口大小（即虚轴半径）有关。通过调整a和b的值，你可以得到不同形状和大小的双曲线。更有趣的是，当a和b相等时，双曲线会变成一个等轴双曲线，其对称性和美感更是达到了极致。

对于中心在原点、焦点在y轴上的双曲线，其标准方程只需将x和y互换即可：

\[ \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 \]

此外，还有中心不在原点、但平行于坐标轴的双曲线方程，以及更一般的双曲线方程形式。这些方程虽然复杂一些，但都是基于上述基本定义和原理推导出来的。

三、双曲线的性质：从基础到深入的探索

双曲线作为一种特殊的曲线，具有许多独特的性质。这些性质不仅在数学上有着广泛的应用，也是理解双曲线本质的关键。

1. 焦点与准线：双曲线的两个焦点是其几何特征的核心。它们之间的距离为2c（其中c^2 = a^2 + b^2）。而双曲线的准线则是两条与x轴（或y轴）平行的直线，它们到原点的距离分别为a^2/c和b^2/c（对于焦点在x轴上的双曲线）。这些准线与双曲线有着密切的关系，是求解双曲线相关问题的重要工具。

2. 渐近线：双曲线还有两条渐近线，它们分别是两条过原点、且与双曲线相切的直线。对于焦点在x轴上的双曲线，其渐近线方程为y = ±(b/a)x。渐近线不仅揭示了双曲线的“极限”形态，还是判断一个点是否在双曲线上的重要依据。

3. 对称性：双曲线具有关于x轴、y轴以及原点的对称性。这种对称性使得双曲线在几何上显得更加优雅和和谐。

4. 离心率：双曲线的离心率e是一个重要的几何量，它等于c/a（其中c^2 = a^2 + b^2）。离心率反映了双曲线的“扁平”程度或“开口”大小。当e接近1时，双曲线接近等轴双曲线；当e增大时，双曲线变得更加“扁平”或“开阔”。

5. 参数方程：除了标准方程外，双曲线还可以用参数方程来表示。对于焦点在x轴上的双曲线，其参数方程为：

\[ \left\{ \begin{array}{l}

x = a\sec\theta \\

y = b\tan\theta \\

\end{array} \right. \]

其中，θ为参数。这个参数方程揭示了双曲线与三角函数之间的紧密联系，为求解双曲线相关问题提供了新的视角和方法。

四、双曲线的应用：从理论到实践的跨越

双曲线不仅在数学上有着丰富的性质和定理，还在物理、工程、天文学等领域有着广泛的应用。

1. 物理学中的应用：在物理学中，双曲线常常用于描述某些物理现象或运动规律。例如，在光学中，双曲线面镜可以产生特定的光线聚焦效果；在力学中，双曲线形状的结构可以承受较大的压力而不变形。

2. 工程学中的应用：在工程领域，双曲线的形状和性质被广泛应用于各种设计之中。例如，双曲线冷却塔利用空气对流原理进行高效散热；双曲线天线则具有良好的方向性和增益性能。

3. 天文学中的应用：在天文学中，双曲线轨道是描述某些天体运动轨迹的重要模型之一。例如，当两个天体以超高速相互接近并掠过对方时，它们的运动轨迹就可能形成一条双曲线轨道。

五、结语：双曲线的魅力与未来

双曲线作为一种独特的数学曲线，以其优雅的形态、丰富的性质和广泛的应用而著称于世。从基础的定义和方程到深入的性质和定理，再到广泛的应用领域，双曲线都展现出了无穷的魅力。

然而，双曲线的研究并未止步于此。随着数学、物理、工程等学科的不断发展，双曲线的新性质、新应用不断涌现出来。例如，在非线性动力学、混沌理论等领域中，双曲线的形态和性质被用于描述复杂系统的行为特征；在计算机图形学和计算机视觉中，双曲线的算法和优化方法也被广泛研究和应用。

因此，我们有理由相信，在未来的科学研究中，双曲线将继续发挥其独特的作用和魅力，引领我们探索更加广阔的数学世界和物理世界。让我们一同期待这场探索之旅的下一个精彩篇章吧！