频率计算公式是怎样的？

在数据分析与信号处理领域，频率计算是一个至关重要的环节。它能够帮助我们理解数据中的周期性变化，揭示隐藏在数据背后的规律。那么，频率计算公式是什么？本文将详细阐述频率计算的基本原理、公式推导、应用场景以及注意事项，旨在为读者提供一个全面而清晰的认识。

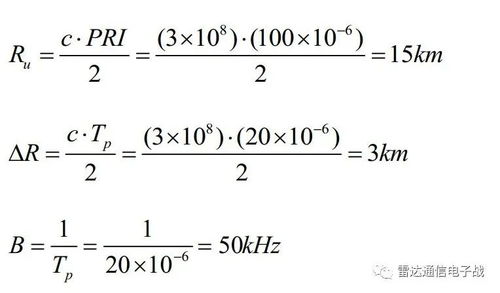
频率，作为描述周期性现象的基本物理量，定义为单位时间内周期性事件发生的次数。在物理学中，频率通常以赫兹（Hz）为单位，即每秒发生的周期数。在数学和信号处理领域，频率的计算通常依赖于对信号波形的分析，特别是波形中的周期长度。

一、频率计算的基本原理

频率计算的核心在于确定信号的周期。周期是指信号完成一个完整循环所需的时间。例如，在一个正弦波中，从波峰到下一个波峰（或波谷到下一个波谷）的时间间隔就是一个周期。一旦周期确定，频率即可通过周期的倒数计算得出。

二、频率计算公式

频率（f）与周期（T）之间的关系可以用以下公式表示：

f = 1/T

这个公式是频率计算的基础。它表明，频率是周期的倒数，即周期越长，频率越低；周期越短，频率越高。

2.1 周期的计算

在实际应用中，周期的测量可能涉及对信号波形的采样和分析。对于离散信号（如数字音频信号），周期可以通过检测相邻峰值（或谷值）之间的样本数来计算，然后将其转换为时间单位（如秒），从而得到周期T。

2.2 频率的精确计算

在信号处理领域，为了获得更精确的频率值，通常需要对信号进行傅里叶变换（Fourier Transform）或快速傅里叶变换（Fast Fourier Transform, FFT）。这些变换能够将信号从时域转换到频域，从而直接读取信号的频率成分。

三、频率计算的应用场景

频率计算在多个领域有着广泛的应用，包括但不限于：

3.1 音频信号处理

在音频信号处理中，频率计算用于分析声音的频谱特性，如基频（即声音的最低频率成分）和谐波成分。这对于语音识别、音乐合成和音频压缩等领域至关重要。

3.2 振动分析

在机械工程领域，频率计算用于分析机械系统的振动特性。通过测量和分析设备的振动频率，可以诊断设备的运行状态，预测潜在的故障，并优化设备的设计和维护。

3.3 通信系统

在通信系统中，频率计算用于确定信号的载波频率、调制频率等关键参数。这对于确保信号的准确传输和接收至关重要。

3.4 生物医学工程

在生物医学工程中，频率计算用于分析生物信号，如心电图（ECG）和脑电图（EEG）中的频率成分。这些分析有助于诊断心血管疾病、神经系统疾病等。

四、频率计算的注意事项

在进行频率计算时，需要注意以下几点：

4.1 信号采样率

信号的采样率对频率计算的准确性有着重要影响。采样率必须足够高，以捕获信号中的所有频率成分。如果采样率过低，可能会导致高频成分的丢失，即所谓的混叠效应。

4.2 噪声干扰

在实际应用中，信号往往受到噪声的干扰。噪声会掩盖信号的真实频率成分，导致频率计算的误差。因此，在进行频率计算之前，通常需要对信号进行滤波处理，以减少噪声的干扰。

4.3 信号的非周期性

对于非周期性信号，频率计算变得复杂。在这种情况下，可能需要采用其他方法（如自相关函数、功率谱密度等）来估计信号的频率特性。

4.4 计算精度与效率

在计算频率时，需要权衡计算精度和计算效率。高精度计算可能需要更多的计算资源和时间，而低精度计算则可能导致结果的不准确。因此，在实际应用中，需要根据具体需求选择合适的计算方法。

五、频率计算方法的优化与创新

随着科技的进步，频率计算方法也在不断优化和创新。例如，现代信号处理算法（如小波变换、希尔伯特-黄变换等）提供了更精细的频率分析能力，能够处理更复杂的信号。此外，随着人工智能和机器学习技术的发展，基于数据驱动的频率预测和分类方法也逐渐崭露头角。

六、总结

频率计算公式f = 1/T是描述周期性现象的基本工具。通过测量信号的周期，我们可以计算出其频率，进而揭示信号中的周期性规律。在多个领域，频率计算都发挥着重要作用，从音频信号处理到振动分析，再到通信系统和生物医学工程。然而，在进行频率计算时，我们需要注意信号采样率、噪声干扰、信号的非周期性以及计算精度与效率等问题。随着科技的进步，频率计算方法也在不断优化和创新，为我们提供了更强大的分析工具。

通过本文的介绍，相信读者对频率计算公式及其应用场景有了更深入的了解。在未来的学习和工作中，我们可以运用这些知识来解决实际问题，推动相关领域的发展。