Excel中轻松掌握标准偏差计算公式

标准偏差（Standard Deviation）是统计学中衡量数据离散程度的重要指标。它描述了数据集中的各个数据点与平均值之间的偏离程度。标准偏差越大，表示数据点之间的离散程度越大；反之，标准偏差越小，表示数据点越集中。在Excel中，标准偏差的计算可以通过内置函数来实现，但了解其背后的计算原理和应用场景同样重要。本文将从标准偏差的定义、计算公式、Excel中的应用以及实际案例等多个维度进行详细阐述。

标准偏差的定义

标准偏差（StdDev, Standard Deviation）是统计学中的一个基本概念，用于量度数据分布的分散程度。它衡量的是数据值偏离算术平均值的程度。在一个数据集中，如果各个数据点与平均值的差异较小，标准偏差就较小；反之，如果各个数据点与平均值的差异较大，标准偏差就较大。标准偏差的大小可以帮助我们了解数据的分布情况，判断数据的稳定性与可靠性。

标准偏差的计算公式

标准偏差的计算过程可以分为几个步骤：

1. 计算平均值：平均值是所有数据点之和除以数据点的总数。

\[

\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

\]

其中，\( \bar{x} \) 表示平均值，\( x_i \) 表示第 \(i\) 个数据点，\( n \) 表示数据点的总数。

2. 计算每个数据点与平均值的差：这一步是为了量化每个数据点偏离平均值的程度。由于差值可能为正也可能为负，直接相加会相互抵消，因此需要对每个差值求平方，使得所有偏差都转化为正数。

3. 计算平方差的平均值（方差）：将上一步得到的所有平方差相加，然后除以数据点的数量（对于样本数据，应除以 \(n-1\) 以修正偏差）。这一步得到的是方差（Variance），它衡量了数据分布的离散程度。

\[

s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2

\]

对于总体数据，方差公式为：

\[

s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2

\]

4. 计算标准偏差：对方差进行平方根运算，即可得到标准偏差。标准偏差的单位与原始数据相同，它直观地表示了数据点与平均值的平均偏离程度。

\[

s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}

\]

对于总体数据，标准偏差公式为：

\[

s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2}

\]

Excel中的应用

在Excel中，标准偏差的计算可以通过内置函数来实现，大大提高了计算效率和准确性。以下是Excel中标准偏差函数的详细介绍：

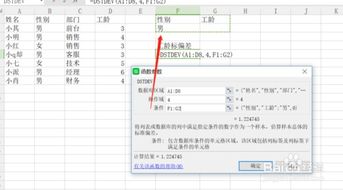
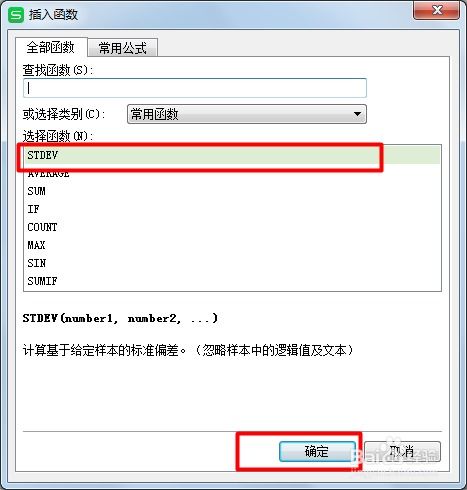
1. STDEV函数：用于计算样本数据的标准偏差。其语法为`STDEV(number1, [number2], ...)`，其中`number1, number2, ...` 是需要计算标准偏差的数据点。如果数据点较多，可以将数据点放入一个数组中，然后通过数组引用进行计算。

2. STDEVP函数：用于计算总体数据的标准偏差。其语法为`STDEVP(number1, [number2], ...)`，与STDEV函数类似，但用于总体数据的计算。

3. STDEV.S函数：这是Excel 2010及以上版本中的新函数，用于计算样本数据的标准偏差，与STDEV函数功能相同。其语法为`STDEV.S(range)`，其中`range`是需要计算标准偏差的数据范围。

4. STDEV.P函数：这是Excel 2010及以上版本中的新函数，用于计算总体数据的标准偏差，与STDEVP函数功能相同。其语法为`STDEV.P(range)`，其中`range`是需要计算标准偏差的数据范围。

实际案例

假设有一组数据`[2, 4, 4, 4, 5, 5, 7, 9]`，我们来计算其样本标准偏差。

1. 计算平均值：

\[

\bar{x} = \frac{2+4+4+4+5+5+7+9}{8} = 5

\]

2. 计算每个数据点与平均值的差并求平方：

\[

(2-5)^2 = 9, \quad (4-5)^2 = 1, \quad (4-5)^2 = 1, \quad (4-5)^2 = 1, \quad (5-5)^2 = 0, \quad (5-5)^2 = 0, \quad (7-5)^2 = 4, \quad (9-5)^2 = 16

\]

3. 计算平方差的平均值（方差）：

\[

s^2 = \frac{9+1+1+1+0+0+4+16}{8-1} \approx 4.29

\]

4. 求平方根得到标准偏差：

\[

s = \sqrt{4.29} \approx 2.07

\]

在Excel中，我们可以直接使用STDEV函数进行计算。假设数据放在A1到A8单元格中，公式为`=STDEV(A1:A8)`，结果为2.07。

标准偏差的应用场景

标准偏差在数据分析中具有举足轻重的地位。它可以帮助我们了解数据的分布情况，判断数据的稳定性与可靠性。在科学实验、市场调研、质量控制等多个领域，标准偏差都扮演着重要的角色。通过计算标准偏差，我们可以评估测量结果的精度，判断不同数据集之间的差异是否显著。

例如，在质量控制中，我们可以通过计算产品尺寸的标准偏差来评估生产过程的稳定性。如果标准偏差较小，说明产品尺寸的一致性较好，生产过程较为稳定；如果标准偏差较大，说明产品尺寸的一致性较差，生产过程可能存在波动，需要进行改进。

结论

标准偏差是一种重要的统计学指标，用于衡量数据的离散程度。通过了解其定义、计算公式以及Excel中的应用，我们可以更好地进行数据分析和决策。在实际应用中，我们可以利用统计软件或编程语言的内置函数来计算标准偏差，提高计算效率和准确性。同时，标准偏差的应用场景广泛，可以帮助我们评估测量结果的精度，判断不同数据集之间的差异是否显著，从而优化决策过程。