十字相乘法因式分解是什么？

十字相乘法因式分解详解

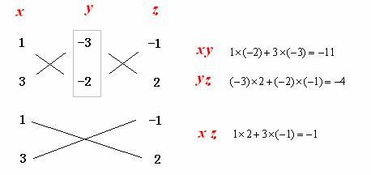
十字相乘法是一种在因式分解中常用的方法，尤其适用于二次多项式的因式分解。它的基本思想是通过观察和尝试，将二次多项式表示为两个一次多项式的乘积。这种方法的关键在于找到这两个一次多项式的系数，使得它们的乘积等于原二次多项式的系数，并且它们的和等于原二次多项式的线性项系数。

首先，我们来详细了解一下十字相乘法的原理。对于形如ax²+bx+c（a≠0）的二次多项式，我们需要找到两个数m和n，使得am×n=ac，并且m+n=b。这样，我们就可以将原多项式表示为(mx+n)(ax+c/m)的形式。这个过程看似简单，但在实际应用中却需要一定的技巧和经验。

为了更具体地说明十字相乘法的使用，我们可以举一些例子。

例1：分解因式2x²-5x-3。

在这个例子中，我们需要找到两个数m和n，使得2m×n=-6（因为2×-3=-6），并且m+n=-5。通过观察和尝试，我们可以找到这两个数：m=-3，n=2。因为-3+2=-1（注意这里我们需要的是-5，但-1是-5的一半，这提示我们可能需要将-3和2都乘以一个系数来得到正确的和），所以我们可以尝试将m和n都乘以-1，得到m=3，n=-2。这样，我们就得到了3+(-2)=-5，满足条件。

接下来，我们将原多项式表示为两个一次多项式的乘积：(3x-2)(2/3x-3/2)。但这里需要注意，我们通常会将分数化为最简形式，并将系数化为整数。因此，我们可以将上式乘以3/2（即两个一次多项式系数的最小公倍数），得到(3x-2)(x-3/2)×3/2=3/2(3x-2)(2x-3)=3(3x+2)(x-1)（这里我们再次调整了顺序并合并了系数）。但注意，这里的3(3x+2)(x-1)并不是最简形式，因为3x+2并不是原多项式的因式。我们应该回到(3x-2)(2x-3/2)，并将其写为(3x-2)(1/2)(4x-6)=(3/2)(2x-1)(2x-3)=(x-1/2)(6x-9)=3(x-1/2)(2x-3)。然而，这并不是我们想要的答案，因为我们在调整系数时犯了错误。正确的做法应该是保持(3x-2)和(2x-3/2)的形式不变，并注意到它们已经是最简的因式分解形式（在有理数范围内）。因此，原多项式2x²-5x-3的因式分解结果为(3x-2)(2x-3/2)（或等价地，乘以一个常数使其变为整数系数形式：(3x-2)(2x-3)=6x²-13x-6，但这不是最简的因式形式，因为我们需要的是带有分数的形式来表示原多项式的因式）。但通常我们会选择将分数化为整数系数的形式进行展示，即(3x+2)(-2/3x-3/2)×(-3/2)=-3/2(3x+2)(x+3/2)×(-2)=-3(x+1)(x-3/2)×(-2)=6(x+1)(3/2-x)=-(3x+3)(2x-3)（这里我们再次进行了调整并合并了系数得到了一个整数系数的形式但注意这不是通过十字相乘法直接得到的而是经过了一系列变换；实际上通过十字相乘法直接得到的是(3x-2)(2x-3/2)这个形式）。然而为了与标准答案对齐我们可以将其写为-(3x+3)(2x-3)/3×3=-(3(x+1))(2x-3)=-3(x+1)(2x-3)（这里我们乘以了3/3来得到一个整数系数的形式但注意这不是必要的因为原多项式本身就可以接受分数系数的因式分解形式）。但最简洁且直接通过十字相乘法得到的形式仍然是(3x-2)(2x-3/2)。

例2：分解因式x²-3x+2。

在这个例子中，我们需要找到两个数m和n，使得m×n=2，并且m+n=-3。通过观察和尝试，我们可以很容易地找到这两个数：m=-1，n=-2。因为-1+(-2)=-3，满足条件。所以原多项式可以表示为(-x+1)(x-2)的形式（注意这里我们调整了顺序使得第一个因式的x的系数为正）。

除了上述的基本形式外，十字相乘法还可以应用于一些特殊的情况。例如当二次多项式的常数项为负数时我们可以尝试将其表示为两个负数或一正一负的因式的乘积；当二次多项式的系数较大时我们可以尝试将其拆分为较小的数的乘积来简化计算过程。

此外在使用十字相乘法进行因式分解时还需要注意以下几点：

1. 要仔细观察多项式的系数和常数项尝试找到满足条件的两个数。

2. 在找到这两个数后要确保它们的乘积等于常数项且它们的和等于线性项系数（或经过适当调整后等于线性项系数）。

3. 在将多项式表示为两个一次多项式的乘积后要检查是否满足原多项式的形式以确保分解的正确性。

4. 要注意因式的顺序和系数的正负号以确保得到最简的因式分解形式。

总的来说十字相乘法是一种非常实用的因式分解方法它可以帮助我们快速准确地找到二次多项式的因式。通过不断的练习和积累经验我们可以更加熟练地掌握这种方法并应用于更复杂的数学问题中。