三角函数常用公式概览

三角函数是数学中的一个基础且极为重要的领域，尤其在几何学、物理学、工程学等领域中，应用广泛。为了深入理解这一数学概念，我们从基础定义、核心公式、应用领域等几个方面展开介绍。

三角函数建立在直角三角形的基础上，通过对比三角形的边长和角度关系，定义了多种函数。最常用的三种三角函数包括正弦（sine，通常表示为sin）、余弦（cosine，通常表示为cos）和正切（tangent，通常表示为tan）。假设有一个直角三角形，其中一个角记作θ，θ的邻边（即与θ角相邻的边）记为a，对边（即与θ角相对的边）记为b，斜边（即最长的边）记为c。那么：

正弦（sinθ）= 对边（b）/ 斜边（c）

余弦（cosθ）= 邻边（a）/ 斜边（c）

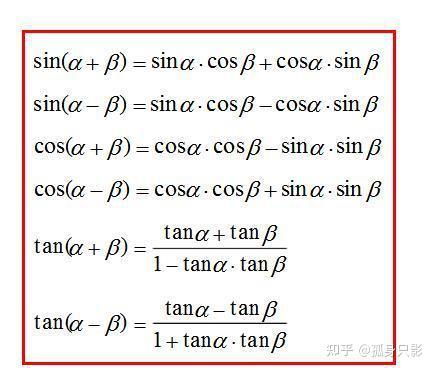
正切（tanθ）= 对边（b）/ 邻边（a）

在角度制中，θ的取值范围是0°到360°；而在弧度制中，θ的取值范围是0到2π。需要注意的是，由于三角函数的周期性，比如在正弦和余弦函数中，2π是它们的基本周期，意味着sin(θ+2π)=sinθ且cos(θ+2π)=cosθ。

基础公式与应用

掌握三角函数的公式是进行复杂计算和解决问题的关键。以下是一些基础的三角函数公式及推导结果：

1. 三角函数的基本关系式：

sin²θ + cos²θ = 1

1 + tan²θ = sec²θ（其中secθ是secant的缩写，secθ=1/cosθ）

1 + cot²θ = csc²θ（其中cotθ是cotangent的缩写，cotθ=1/tanθ；cscθ是cosecant的缩写，cscθ=1/sinθ）

这些公式可以从三角函数的定义中直接推导出来，通过简单的几何关系和代数变换，揭示了三角函数之间内在联系。

2. 两角和与差的三角函数公式：

sin(α±β) = sinαcosβ ± cosαsinβ

cos(α±β) = cosαcosβ ∓ sinαsinβ（注意“∓”符号代表“-”或“+”，分别与“±”相对应）

tan(α±β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)

这些公式揭示了当两个角度进行加或减运算时，三角函数值的变化规律。它们是许多三角函数恒等式的基础，对于复杂表达式的化简与计算具有重要作用。

3. 倍角公式：

sin2θ = 2sinθcosθ

cos2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ

tan2θ = (2tanθ) / (1 - tan²θ)

倍角公式常用于化简复杂三角函数表达式或解决特定的数学问题。这些公式通过对原函数进行运算，找出了二倍角函数的简单表达形式。

4. 半角公式：

sin(θ/2) = ±√[(1 - cosθ) / 2]

cos(θ/2) = ±√[(1 + cosθ) / 2]

tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)] = (1 - cosθ) / sinθ = sinθ / (1 + cosθ)

半角公式利用已知的三角函数值来求解对应角度的一半的三角函数值，尤其当面对求解某个特定角度一半的三角函数时，非常实用。

5. 积化和差公式与和差化积公式：

积化和差：sinαcosβ = [sin(α+β) + sin(α-β)] / 2；cosαsinβ = [sin(α+β) - sin(α-β)] / 2；cosαcosβ = [cos(α+β) + cos(α-β)] / 2；sinαsinβ = -[cos(α+β) - cos(α-β)] / 2

和差化积：sinα + sinβ = 2sin[(α+β)/2]cos[(α-β)/2]；sinα - sinβ = 2cos[(α+β)/2]sin[(α-β)/2]；cosα + cosβ = 2cos[(α+β)/2]cos[(α-β)/2]；cosα - cosβ = -2sin[(α+β)/2]sin[(α-β)/2]

这些公式帮助我们在遇到乘积或和差形式的三角函数时，能更有效地转化为更简单或更易处理的形式。

实际应用

三角函数在实际问题中用途广泛，涵盖诸多领域：

物理学：在物理学中，三角函数经常用于解决振动、波动、力和运动等问题。例如，弹簧振子的位移随时间的变化，可以利用正弦函数来描述。

工程学：在工程领域，三角函数在测量、绘图、计算与设计等方面都有应用。工程师常用三角函数来解决空间问题，如斜面的长度、高度计算等。

地理学：地理学中，三角函数对于测量地表物体的位置和距离非常有用。通过地球经纬度的信息，我们可以使用三角函数计算出任意两点之间的距离。

计算机科学：在计算机图形学、动画和计算机视觉中，三角函数帮助开发人员理解和操作角度和旋转。游戏开发中的相机角度、动画角色的移动与旋转等都离不开三角函数。

天文学：三角函数在天文学中也有重要作用，尤其在星体位置的确定、天体轨迹的计算等方面。通过观察与计算，科学家们可以利用三角函数推导出恒星的位置、距离以及运行规律。

通过对三角函数基础定义的了解、掌握其基础公式及应用方法，我们不仅能够更有效地解决数学问题，还能为相关领域的学习与工作打下坚实的基础。无论是学习其他学科，还是解决实际生活中的问题，掌握三角函数都会极大地提高我们的思维能力和解决复杂问题的能力。