电感是如何计算的？

电感是电子学中的一个重要概念，广泛应用于各种电路和设备中。了解电感的计算公式不仅能帮助我们更好地设计和分析电路，还能在实际应用中提高电路的性能和稳定性。本文将详细介绍电感的计算公式，并通过实例展示其应用方法。

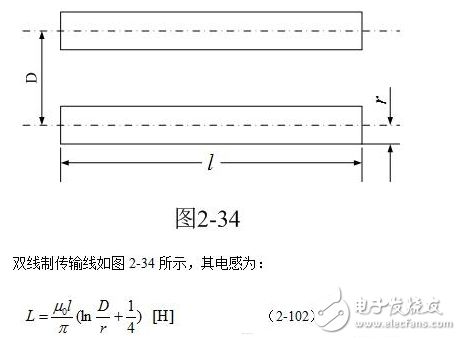
电感的基本概念

电感（Inductance）是衡量一个电路元件能够产生磁场或由于磁场变化而产生电动势的物理量。其符号为“L”，单位为“亨利”（H）。电感器件通常包括线圈、电感器和变压器等。电感的作用主要体现在存储磁场能量、滤波、稳定电流和电压等方面。

电感的计算公式

电感的计算公式主要取决于其物理结构和工作条件。以下是几种常见的电感计算公式及其应用场景：

1. 单层线圈电感计算公式

对于简单的单层线圈，其电感计算公式如下：

\[L = \frac{\mu_0 \cdot N^2 \cdot A}{l}\]

其中：

\(L\) 是电感，单位为亨利（H）。

\(\mu_0\) 是真空中的磁导率，其值为 \(4\pi \times 10^{-7}\) H/m。

\(N\) 是线圈的匝数。

\(A\) 是线圈的面积，单位为平方米（m²）。

\(l\) 是线圈的长度，单位为米（m）。

该公式适用于导线均匀绕制且匝数较少的单层线圈。

2. 多层线圈电感计算公式

多层线圈的电感计算相对复杂，可以使用经验公式或查表法。一种常见的多层线圈电感经验公式为：

\[L = K_N \cdot K_A \cdot \mu_0 \cdot \frac{N^2 \cdot d^2}{18d + 40l}\]

其中：

\(K_N\) 是匝数系数，通常取值为 0.96 至 1.02。

\(K_A\) 是面积系数，根据线圈的形状和排列方式取值。

\(d\) 是线圈的平均直径，单位为米（m）。

\(l\) 是线圈的导线直径，单位为米（m）。

3. 环形线圈电感计算公式

环形线圈的电感计算公式为：

\[L = \mu_0 \cdot \mu_r \cdot \frac{N^2 \cdot A}{l}\]

其中：

\(\mu_r\) 是相对磁导率，是线圈材料相对于真空的磁导率。

环形线圈常用于滤波器和高频电路中，由于其结构紧凑、电感值稳定，被广泛应用。

4. 螺线管电感计算公式

螺线管（Solenoid）是一种特殊的线圈结构，其电感计算公式为：

\[L = \mu_0 \cdot \frac{N^2 \cdot A}{l}\left(1 - \frac{k}{l}\ln\left(\frac{l}{k}\right) - \frac{1}{2}\right)\]

其中：

\(k\) 是螺线管的长度与半径的比值。

螺线管常用于电磁铁和电磁继电器中，其电感值较大，可以产生较强的磁场。

电感计算公式的应用实例

为了更好地理解电感的计算公式，下面通过几个实例进行展示：

实例1：单层线圈电感计算

设计一个单层线圈，导线直径为1mm，线圈直径为10cm，匝数为100匝。计算其电感值。

1. 计算线圈面积 \(A\)：

\[A = \pi \left(\frac{10 \times 10^{-2}}{2}\right)^2 = 7.854 \times 10^{-3} \text{ m}^2\]

2. 计算线圈长度 \(l\)：

\[l = \pi \times 10 \times 10^{-2} = 0.314 \text{ m}\]

3. 代入单层线圈电感公式：

\[L = \frac{4\pi \times 10^{-7} \times 100^2 \times 7.854 \times 10^{-3}}{0.314} = 31.4 \text{ μH}\]

实例2：环形线圈电感计算

设计一个环形线圈，导线直径为1mm，线圈平均直径为10cm，匝数为200匝，使用相对磁导率为1000的材料。计算其电感值。

1. 计算线圈面积 \(A\)：

\[A = \pi \left(\frac{10 \times 10^{-2}}{2}\right)^2 = 7.854 \times 10^{-3} \text{ m}^2\]

2. 代入环形线圈电感公式：

\[L = 4\pi \times 10^{-7} \times 1000 \times 200^2 \times 7.854 \times 10^{-3} = 40.19 \text{ mH}\]

实例3：螺线管电感计算

设计一个螺线管，导线直径为1mm，螺线管长度为1m，半径为0.05m，匝数为500匝。计算其电感值。

1. 计算 \(k\) 值：

\[k = \frac{1}{0.05} = 20\]

2. 计算 \(\frac{k}{l}\ln\left(\frac{l}{k}\right)\)：

\[\frac{k}{l}\ln\left(\frac{l}{k}\right) = \frac{20}{1}\ln\left(\frac{1}{20}\right) \approx -4.605\]

3. 代入螺线管电感公式：

\[L = 4\pi \times 10^{-7} \times 500^2 \times \pi \left(0.05\right)^2 \left(1 + 4.605 - 0.5\right) = 47.12 \text{ mH}\]

总结

电感作为电子学中的重要元件，其计算公式在实际应用中起着至关重要的作用。通过了解不同形状和结构的线圈电感计算公式，可以精确计算电感值，从而设计和优化电路性能。本文介绍了单层线圈、多层线圈、环形线圈和螺线管的电感计算公式，并通过实例展示了其应用方法。希望这些内容能帮助读者更好地理解和应用电感计算公式，提高电路设计和分析的能力。