二重积分公式大全有哪些？共24个

在微积分领域中，二重积分是一个至关重要的概念，它广泛应用于计算面积、体积、质量分布以及物理场（如电场、重力场）的势能等问题。二重积分不仅深化了我们对积分学的理解，也为解决复杂问题提供了强有力的工具。本文将详细介绍24个常见的二重积分公式，旨在帮助读者系统地掌握这一领域的知识。

一、基本二重积分公式

1. 直角坐标系下的基本公式：

\[

\iint_D f(x,y) \,dA = \int_a^b \left( \int_c^{d(x)} f(x,y) \,dy \right) \,dx

\]

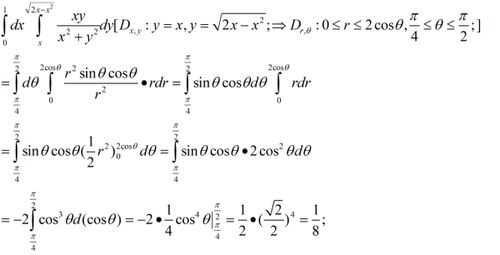
或

\[

\iint_D f(x,y) \,dA = \int_c^d \left( \int_{a(y)}^{b(y)} f(x,y) \,dx \right) \,dy

\]

其中，\(D\) 是积分区域，\(a, b, c, d\) 以及 \(d(x), a(y), b(y)\) 是区域的边界。

2. 极坐标系下的基本公式：

\[

\iint_D f(r,\theta) \,r \,dr \,d\theta

\]

其中，\(r\) 是原点到点的距离，\(\theta\) 是与正x轴的夹角。

二、特定几何形状的二重积分

3. 矩形区域：

\[

\iint_R f(x,y) \,dA = \int_a^b \int_c^d f(x,y) \,dy \,dx

\]

其中，\(R\) 是由 \(a \leq x \leq b\) 和 \(c \leq y \leq d\) 定义的矩形区域。

4. 圆形区域：

在极坐标系下，对半径为 \(r_0\) 的圆进行积分：

\[

\iint_C f(r,\theta) \,r \,dr \,d\theta = \int_0^{2\pi} \int_0^{r_0} f(r,\theta) \,r \,dr \,d\theta

\]

5. 环形区域：

对于内外半径分别为 \(r_1\) 和 \(r_2\) 的环形区域：

\[

\iint_A f(r,\theta) \,r \,dr \,d\theta = \int_0^{2\pi} \int_{r_1}^{r_2} f(r,\theta) \,r \,dr \,d\theta

\]

三、变上限积分与二重积分的关系

6. 通过变上限积分求二重积分：

对于某些特定情况，可以通过对变上限积分再次积分来求解二重积分。

四、积分区域的变换

7. 坐标变换（雅可比行列式）：

若进行坐标变换 \(u = u(x,y)\), \(v = v(x,y)\)，则

\[

\iint_D f(x,y) \,dA = \iint_{D'} f(u^{-1}(u,v), v^{-1}(u,v)) |J| \,du \,dv

\]

其中，\(J\) 是雅可比行列式。

五、对称性简化积分

8. 关于原点对称：

若函数 \(f(x,y)\) 关于原点对称，则

\[

\iint_D f(x,y) \,dA = 0 \quad \text{（若 \(f(x,y)\) 是奇函数）}

\]

或

\[

\iint_D f(x,y) \,dA = 2 \iint_{D^+} f(x,y) \,dA \quad \text{（若 \(f(x,y)\) 是偶函数）}

\]

其中，\(D^+\) 是 \(D\) 的上半部分。

9. 关于y轴对称、关于x轴对称的情况类似，可通过简化积分区域来减少计算量。

六、积分中值定理与二重积分

10. 二重积分的中值定理：

在 \(D\) 上存在一个点 \((x_0, y_0)\)，使得

\[

\iint_D f(x,y) \,dA = f(x_0, y_0) \cdot A(D)

\]

其中，\(A(D)\) 是 \(D\) 的面积。

七、物理应用中的二重积分

11. 计算质量：

\[

M = \iint_D \rho(x,y) \,dA

\]

其中，\(\rho(x,y)\) 是密度函数。

12. 计算质心：

\[

\bar{x} = \frac{\iint_D x\rho(x,y) \,dA}{M}, \quad \bar{y} = \frac{\iint_D y\rho(x,y) \,dA}{M}

\]

13. 计算转动惯量：

\[

I = \iint_D r^2 \rho(x,y) \,dA

\]

其中，\(r\) 是点 \((x,y)\) 到某轴的距离。

八、格林公式及其应用

14. 格林公式：

对于简单闭合曲线 \(C\) 及其内部区域 \(D\)，有

\[

\oint_C (Pdx + Qdy) = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \,dA

\]

15. 格林公式的应用：

可用于求解某些类型的线积分，或通过线积分求解面积。

九、其他特殊二重积分公式

16. 极坐标下的扇形区域：

对于中心角为 \(\alpha\) 的扇形区域：

\[

\iint_S f(r,\theta) \,r \,dr \,d\theta = \int_0^\alpha \int_0^{r_0} f(r,\theta) \,r \,dr \,d\theta

\]

17. 椭圆区域：

通过坐标变换将椭圆区域转换为圆形区域进行积分。

18. 抛物线区域：

利用抛物线的方程进行坐标变换。

19. 双曲线区域：

类似地，通过坐标变换进行积分。

20. 分段定义函数：

对于在不同区域有不同定义的函数，需要分段进行积分。

21. 含有参数的二重积分：

当被积函数中含有参数时，先对自变量积分，再对参数积分。

22. 利用对称性简化：

利用函数关于坐标轴的对称性简化积分过程。

23. 改变积分次序：

有时改变积分的次序可以简化计算。

24. 复杂区域的分割：

对于复杂区域，可以将其分割为多个简单区域分别进行积分，然后求和。

结语

二重积分不仅是微积分的重要组成部分，也是解决实际问题的有力工具。通过掌握上述24个公式及其应用场景，读者可以更加灵活和高效地运用二重积分解决实际问题。无论是计算几何量、物理量还是进行理论分析，二重积分都展现出其独特的魅力和广泛的应用价值。希望本文能为读者提供一个全面且深入的二重积分知识框架，助力其在相关领域的学习和研究中取得更大的进步。