圆的面积计算公式推导过程

圆的面积推导公式是数学中一个基础且重要的概念，它不仅在数学学科内占据核心地位，也是物理学、工程学等多个领域不可或缺的工具。本文将详细介绍圆面积推导公式的来源、步骤及其在实际中的应用，旨在帮助读者深入理解这一基本几何概念。

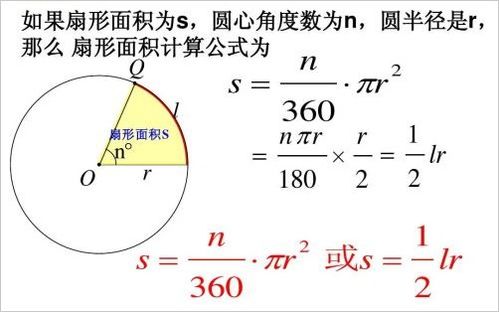
圆的面积推导：从直观到抽象

圆的面积是指一个平面内，所有与圆心距离相等的点所组成的封闭图形的内部空间大小。直观上，我们知道圆的面积与其半径有关，但具体如何量化这一关系，则需要通过数学推导。

1. 直观感受与猜想

最早对圆面积进行探索的是古代数学家。他们通过观察不同大小的圆，发现半径越大的圆占据的平面空间也越大。基于这一直观感受，他们猜想圆的面积与半径的平方成正比。这一猜想为后来的严格证明提供了方向。

2. 割圆术：从多边形逼近圆

为了验证这一猜想，古代数学家采用了割圆术的方法。割圆术的核心思想是将圆分割成若干个小扇形，然后将这些扇形重新排列组合成一个近似的多边形。随着分割的扇形数量增加，这个多边形越来越接近一个真正的圆。通过计算这个多边形的面积，可以近似地得到圆的面积。

古希腊数学家阿基米德是割圆术的杰出代表。他通过不断增加分割的扇形数量，发现多边形面积逐渐收敛于一个固定的值。这一值即为圆的面积。阿基米德的方法虽然繁琐，但为后来微积分的发展奠定了基础。

3. 微积分方法：精确推导

随着微积分的发明，圆的面积推导变得更加精确和简洁。微积分提供了一种将圆分割成无限多个微小部分，然后求和得到总面积的方法。

具体来说，我们可以将圆看作是一个半径为r的曲线y=√(r^2-x^2)与x轴围成的区域。利用定积分的性质，我们可以写出圆的面积公式：

S = ∫[-r, r] √(r^2 - x^2) dx

这个积分表示的是从-r到r，曲线y=√(r^2-x^2)与x轴围成的面积。通过求解这个定积分，我们可以得到圆的面积公式为S = πr^2。

圆的面积公式：π的奥秘

在上述推导过程中，我们遇到了一个神秘的常数π（圆周率）。π是一个无理数，它的小数部分是无限不循环的。尽管π的值无法精确表示为一个有限小数或分数，但它在圆的面积、周长以及许多其他几何和物理问题中都扮演着至关重要的角色。

1. π的定义与计算

π的定义有多种方式，其中一种常见的方式是通过圆的周长与直径的比值来定义。即π = C/d，其中C是圆的周长，d是圆的直径。另一种等价的方式是通过圆的面积与半径平方的比值来定义π，即π = S/r^2。

在实际计算中，我们通常使用π的近似值，如3.14159等。随着计算机技术的发展，我们可以计算π到小数点后数百万位甚至更多位。然而，无论计算到多少位，π仍然是一个无理数，它的小数部分永远不会循环或终止。

2. π在圆面积公式中的应用

在圆的面积公式S = πr^2中，π起到了一个缩放因子的作用。它确保了无论圆的半径如何变化，面积总是与半径的平方成正比。这一性质使得圆的面积公式在解决实际问题时具有广泛的适用性。

圆面积公式的应用

圆的面积公式在数学、物理学和工程学等多个领域都有广泛的应用。

1. 数学领域

在数学领域，圆的面积公式是几何学的基础之一。它不仅可以用来计算圆的面积，还可以作为推导其他几何图形面积的基础。例如，在计算圆环（两个同心圆之间的区域）的面积时，我们需要用到圆的面积公式。此外，在解析几何和微积分中，圆的面积公式也是求解某些积分和极限问题的重要工具。

2. 物理学领域

在物理学领域，圆的面积公式在描述圆形物体的物理性质时起着关键作用。例如，在计算圆的周长、表面积或体积时，我们都需要用到圆的面积公式。此外，在波动学、光学和电磁学等领域中，圆的面积公式也经常出现。它帮助我们理解波的传播、光的散射和电磁场的分布等物理现象。

3. 工程学领域

在工程学领域，圆的面积公式在设计和制造圆形零件时具有重要意义。例如，在计算圆柱体的侧面积和底面积时，我们需要用到圆的面积公式。此外，在管道流动、轮轴转动和齿轮啮合等问题中，圆的面积公式也是求解的关键之一。它帮助我们优化零件的设计，提高系统的性能和效率。

结语

圆的面积推导公式是数学中一个经典而重要的问题。通过从直观感受到严格证明的过程，我们不仅理解了圆面积与半径之间的关系，还深入探讨了π这一神秘常数的奥秘。圆的面积公式在数学、物理学和工程学等多个领域都有广泛的应用，它帮助我们解决实际问题，推动科学和技术的发展。因此，深入理解和掌握圆的面积推导公式对于我们每一个人来说都是至关重要的。