对数的基本公式及其定义

在数学的浩瀚宇宙中，对数（Logarithm，简称Log）无疑是一颗璀璨的星辰，它不仅照亮了数学理论的殿堂，也深刻地影响着科学探索的每一个角落，从物理学中的声强级计算到生物学中种群增长的模型，再到计算机科学中的数据压缩与加密技术，对数的身影无处不在。那么，何为对数的基本公式？让我们一同揭开它神秘的面纱，探索这一数学工具背后的逻辑与魅力。

对数的起源与定义

故事的起点，可以追溯到17世纪初的苏格兰数学家约翰·纳皮尔（John Napier），他为了解决当时天文学计算中繁琐的乘法问题，创造性地发明了“对数”这一概念。简单来说，对数是一种将乘法运算转化为加法运算（或除法运算转化为减法运算）的数学工具，极大地简化了复杂数值的计算过程。

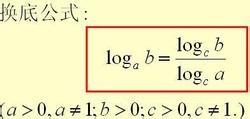
对数的基本定义如下：若a^x = N（a > 0，且a ≠ 1），则称x是以a为底N的对数，记作x = logₐN。这里，a被称为对数的底数，N称为真数，x则是对应的对数值。通过这个定义，我们可以看到，对数实际上是指数运算的逆运算。

对数的基本公式

在深入了解对数的基本公式之前，先记住几个关键的对数性质，它们将是我们探索之旅的灯塔：

1. 换底公式：

\[

\log_{b}a = \frac{\log_{c}a}{\log_{c}b}

\]

其中，c可以是任意正数且c ≠ 1。这个公式允许我们在不同底数之间转换对数，极大地增加了对数运算的灵活性。

2. 对数的乘法性质：

\[

\log_{a}(mn) = \log_{a}m + \log_{a}n

\]

这一性质将乘法运算转化为加法运算，是对数最直观也是最重要的应用之一。

3. 对数的除法性质：

\[

\log_{a}\left(\frac{m}{n}\right) = \log_{a}m - \log_{a}n

\]

与乘法性质相对应，除法性质将除法运算简化为减法运算。

4. 对数的幂的性质：

\[

\log_{a}(m^n) = n\log_{a}m

\]

此性质表明，当我们在真数上应用幂运算时，可以在对数值上乘以相应的指数，从而实现复杂的幂运算的简化。

5. 零与一对数的特殊性：

对于任何正数a（a ≠ 1），有 \(\log_{a}1 = 0\)，因为任何数的0次方都是1。

另外，不存在\(\log_{a}0\)的值，因为没有任何数的正数次方能等于0（注意，负数次方或分数次方可能导致无限大或复数结果，但这不属于基本对数的讨论范畴）。

对数公式的应用实例

了解了这些基本公式和性质后，我们来看几个应用实例，感受对数在解决实际问题中的威力。

例1： 简化计算。假设我们需要计算 \(2^{10} \times 2^{15}\)，直接计算可能相对繁琐。但利用对数的乘法性质，我们可以将其转化为：

\[

\log_{2}(2^{10} \times 2^{15}) = \log_{2}2^{10} + \log_{2}2^{15} = 10 + 15 = 25

\]

由此得知，\(2^{10} \times 2^{15} = 2^{25}\)，大大简化了计算过程。

例2： 求解方程。考虑方程 \(4^x = 16\)，传统解法可能需要试错或复杂的代数变换。但利用对数的定义，我们可以直接得到：

\[

x = \log_{4}16

\]

由于 \(4^2 = 16\)，所以 \(x = 2\)。

例3： 数据分析。在金融分析中，对数经常被用来表示增长率或衰减率，因为对数能够平滑极端值对整体趋势的影响，使得数据更加易于分析和预测。

结语

对数的基本公式，不仅仅是数学符号的堆砌，它们是连接现实世界与数学抽象世界的桥梁，是简化复杂计算、深化科学理解的利器。从纳皮尔最初的发明到如今广泛应用于各个领域的现代对数理论，对数的故事仍在继续。希望这篇文章能够激发你对对数世界的好奇与探索欲，让你在数学的海洋中遨游时，能更加自如地运用这一强大的数学工具。