揭秘棱锥体积公式，轻松掌握计算方法

棱锥，作为一种常见的三维几何体，在数学、物理及工程学中有着广泛的应用。它的体积计算是几何学中的一个基本问题，对于理解空间几何结构及其性质具有重要意义。本文旨在深入探讨棱锥的体积公式，通过解释棱锥的基本概念、推导体积公式的过程，以及提供实际应用示例，使读者能够全面理解并掌握这一几何概念。

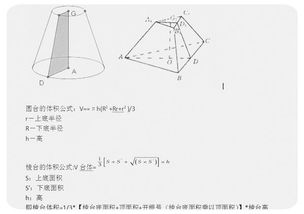
棱锥的定义与基本特性

棱锥是一种具有一个多边形底面与若干个三角形侧面的多面体。其中，底面的各顶点与顶面（通常为一个点，称为顶点或锥尖）相连，形成三角形侧面。棱锥的分类依据底面形状的不同，可以分为三棱锥（底面为三角形）、四棱锥（底面为四边形）、五棱锥等。特别地，当底面为正多边形，且顶点到底面各边的垂直距离相等时，棱锥被称为正棱锥。

棱锥的体积公式

棱锥的体积公式是几何学中的一个基本定理，其表达式为：

V = (1/3) * h * S

其中，V表示棱锥的体积，h是棱锥的高（即从顶点到底面的垂直距离），S是底面的面积。这个公式表明，棱锥的体积等于其高与底面积乘积的三分之一。

公式的推导

棱锥体积公式的推导可以通过积分、相似三角形或几何构造等多种方法来实现。以下提供一种基于相似三角形的直观推导方法：

设想棱锥被平行于底面的一个平面切割，形成一个小的相似棱锥和一个新的棱台。由于切割面与底面平行，新形成的小棱锥与原棱锥在形状上是相似的，且底面面积之比等于高的平方比。设小棱锥的体积为V1，高为h1，底面面积为S1；原棱锥的体积为V，高为h，底面面积为S。则有：

V1/V = (h1/h)^3 = S1/S

从上式可以解出V1与V的关系。当我们将棱锥无限细分，每次切割都得到一个新的更小的相似棱锥，直到顶点为止。所有这些小棱锥的体积之和就是原棱锥的体积。由于每个小棱锥的体积都是其高与底面积乘积的三分之一，通过积分（在离散情况下为求和）可以得出原棱锥的体积公式为V = (1/3) * h * S。

公式的应用

棱锥体积公式在解决实际问题中具有广泛的应用。以下是一些具体示例：

1. 工程测量：在建筑设计中，经常需要计算屋顶、塔架等结构物的体积，这些结构物往往可以近似为棱锥形状。通过测量底面面积和高，即可利用棱锥体积公式快速计算出体积。

2. 地质勘探：在矿产资源勘探中，经常需要对地下矿体进行体积估算。当矿体形状近似为棱锥时，可以通过测量矿体的底面面积和平均高度，利用棱锥体积公式进行估算。

3. 物理学应用：在物理学中，棱锥体积公式可以用于计算电磁场、重力场等物理量在棱锥形状区域内的积分值。例如，在静电学中，可以通过计算带电棱锥所产生的电场能量来验证棱锥体积公式的正确性。

4. 数学教育：在数学教学中，棱锥体积公式是几何学课程的重要组成部分。通过学习棱锥体积公式的推导和应用，可以帮助学生培养空间想象力、逻辑思维能力和数学应用能力。

特殊棱锥的体积计算

对于特殊形状的棱锥，如正棱锥、直角棱锥等，其体积计算可以通过简化底面面积或利用特殊性质来实现。

1. 正棱锥：正棱锥的底面是正多边形，且侧面都是全等的等腰三角形。通过计算正多边形的面积，即可利用棱锥体积公式计算出正棱锥的体积。

2. 直角棱锥：直角棱锥的底面是一个矩形，且侧棱与底面垂直。在这种情况下，可以直接计算底面的面积和高，然后利用棱锥体积公式进行计算。

3. 斜棱锥：斜棱锥的底面是任意多边形，且侧棱不垂直于底面。为了计算斜棱锥的体积，需要首先找到从顶点到底面的垂线（即高），这通常需要通过几何构造或向量运算来实现。然后，计算底面的面积和高，即可利用棱锥体积公式进行计算。

棱锥体积公式的证明与验证

除了上述基于相似三角形的推导方法外，棱锥体积公式还可以通过其他方法进行证明和验证。例如，可以利用微积分中的三重积分或柱面坐标系等方法进行证明；也可以通过实验测量棱锥的体积，并与理论计算结果进行比较来验证公式的正确性。

需要注意的是，在实验测量中，由于测量误差和实验条件等因素的影响，实验结果可能与理论计算结果存在一定的偏差。因此，在实验验证时，需要采用精密的测量仪器和方法，并尽可能减小误差的影响。

总结与展望

棱锥体积公式是几何学中的一个基本定理，