梯形体积的计算公式是什么？

梯形，作为一种常见的几何形状，在日常生活和工程应用中屡见不鲜。无论是建筑设计中的屋顶斜面，还是水利工程中的堤坝横截面，梯形都以其独特的形态发挥着重要作用。然而，当我们试图计算梯形的体积时，很多人可能会感到困惑，因为梯形本身是一个二维图形，而体积则是三维空间中的概念。那么，梯形体积的计算究竟是如何进行的呢？本文将深入探讨这一问题，并揭示梯形体积公式的奥秘。

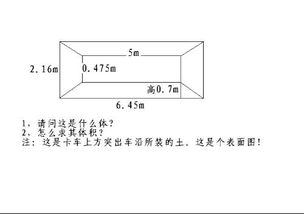
首先，我们需要明确一点：梯形本身并没有直接的体积公式，因为它是一个二维图形。但是，当我们把梯形作为一个三维物体的底面时，就可以通过计算这个三维物体的体积来间接得到与梯形相关的体积。这里，我们主要讨论的是两种常见的三维物体：棱柱和棱台。

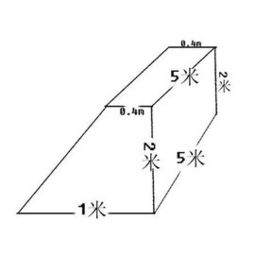
棱柱中的梯形体积

棱柱是一种顶面与底面平行、相似且等大的多面体。当棱柱的底面为梯形时，我们称之为梯形棱柱。为了计算梯形棱柱的体积，我们可以使用以下公式：

体积 = 底面积 × 高

其中，底面积即为梯形的面积，高则是棱柱的高。

梯形的面积公式为：

面积 = (上底 + 下底) × 高 ÷ 2

将梯形面积公式代入棱柱体积公式中，我们得到：

梯形棱柱体积 = (上底 + 下底) × 梯形的高 ÷ 2 × 棱柱的高

这里需要注意的是，梯形的高（用于计算梯形面积）与棱柱的高（垂直于底面的高度）是两个不同的概念，但在某些情况下，它们可能重合或相关。

棱台中的梯形体积

棱台是一种由两个平行且相似的多边形底面以及连接这两个底面的侧面围成的多面体。当棱台的底面为梯形时，我们称之为梯形棱台。梯形棱台的体积计算稍微复杂一些，但同样基于底面积和高的概念。

梯形棱台的体积公式为：

体积 = 1/3 × 高 × (上底面积 + 下底面积 + 上下底面积的平方根乘积)

其中，上底面积和下底面积分别是梯形棱台的上底和下底的面积，它们都可以使用梯形面积公式来计算。而上下底面积的平方根乘积则是指上底面积的平方根与下底面积的平方根的乘积。

为了更直观地理解这个公式，我们可以将其拆分为两部分：

1. 首先计算上底和下底的平均面积，即 (上底面积 + 下底面积) ÷ 2。

2. 然后，将这个平均面积乘以一个修正因子（1 + √(上底面积/下底面积) ÷ 2），这个修正因子考虑了上底和下底面积的差异对体积的影响。

3. 最后，将上述结果乘以棱台的高，得到梯形棱台的体积。

然而，在实际应用中，我们通常会直接使用梯形棱台的体积公式进行计算，而不是通过上述拆分步骤。这是因为直接应用公式可以更快地得到结果，而且公式本身已经包含了所有必要的修正因子。

梯形体积公式的应用

梯形体积公式在多个领域都有广泛的应用。以下是一些具体的例子：

1. 建筑设计：在建筑设计中，梯形棱柱和棱台常用于创建独特的屋顶形状和墙体结构。通过计算梯形体积，设计师可以确保这些结构的稳定性和美观性。

2. 水利工程：在水利工程中，梯形棱台常用于模拟堤坝的横截面。通过计算梯形棱台的体积，工程师可以评估堤坝的储水能力和稳定性。

3. 土木工程：在土木工程中，梯形棱柱和棱台也常用于道路、桥梁和隧道的设计。通过计算梯形体积，工程师可以确定这些结构的材料需求和施工难度。

4. 制造业：在制造业中，梯形棱柱和棱台形状的零件和组件很常见。通过计算梯形体积，制造商可以优化材料使用和生产流程。

梯形体积公式的局限性

尽管梯形体积公式在多个领域都有广泛的应用，但它也存在一些局限性。以下是一些需要注意的问题：

1. 形状限制：梯形体积公式仅适用于梯形作为底面的棱柱和棱台。对于其他形状的三维物体，需要使用不同的体积公式。

2. 精度问题：在实际应用中，由于测量误差和形状复杂性等因素，梯形体积公式的计算结果可能存在一定的精度问题。因此，在使用公式时需要注意数据的准确性和可靠性。

3. 适用范围：梯形体积公式主要适用于静态和刚性的三维物体。对于动态或柔性的物体（如流体或弹性体），需要使用不同的方法来计算体积。

结论

综上所述，梯形体积的计算并不是直接通过梯形本身进行的，而是通过将梯形作为三维物体的底面来间接计算。对于梯形棱柱和棱台这两种常见的三维物体，我们可以使用相应的体积公式来计算它们的体积。这些公式基于底面积和高的概念，并考虑了上底和下底面积的差异对体积