三角函数cot的定义及公式是什么？

三角函数cot，全称为余切函数，是数学中三角学领域的一个重要概念。在介绍cot的公式之前，我们先来了解一下三角函数的基础知识。三角函数通常用于描述直角三角形中边长与角度之间的关系，主要包括正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc）六种。这些函数在解决几何、物理及工程问题时具有广泛的应用。

余切函数cot，定义为任意角α的终边上的一个点在直角三角形中的邻边长度除以对边长度，即cotα = 邻边 / 对边。在直角三角形ABC中，若角C为直角，角A为α，那么cotα = AC / AB，其中AC为邻边，AB为对边。然而，这种定义方式仅适用于0° < α < 90°的第一象限角。为了扩展到所有象限的角，我们可以使用cot的诱导公式或与其他三角函数的关系来定义。

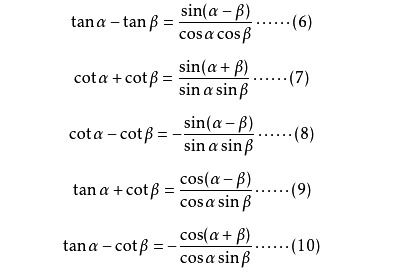
cot的诱导公式基于三角函数在各象限的符号和关系。对于任意角α，我们可以根据其所处的象限，利用正弦和余弦的关系来推导cot的值。例如，当α为第二象限角时，我们可以将其转化为第一象限角（180° - α）的余弦除以正弦，即cotα = -cos(180° - α) / sin(180° - α) = -cosα / sinα（因为在第二象限，余弦为负，正弦为正）。类似地，我们可以推导出cot在第三象限和第四象限的值。

但更常用的方法是利用cot与其他三角函数的关系。根据三角函数的定义和性质，我们有cotα = 1 / tanα。这意味着，cot函数是tan函数的倒数。这一关系使得cot函数的计算变得相对简单，因为tan函数的值在许多情况下是已知的或容易计算的。

在进一步探讨cot的公式时，我们需要提及一些重要的恒等式和变换公式。这些公式在解决三角问题时非常有用，可以帮助我们简化表达式、解方程或证明定理。

首先是cot的倍角公式。倍角公式允许我们通过已知的单角三角函数值来计算双角的三角函数值。对于cot函数，我们有cot2α = (cot²α - 1) / (2cotα)。这个公式可以通过cot的定义和tan的倍角公式推导出来。

接下来是cot的半角公式。半角公式与倍角公式相反，它允许我们通过双角的三角函数值来计算单角的三角函数值。对于cot函数，我们有cot(α/2) = 1 + cosα / sinα = (1 + cosα) / sinα = 2cos²(α/2) / 2sin(α/2)cos(α/2) = cos(α/2) / sin(α/2) = cot(π/4 - α/2)（这里利用了sin²θ + cos²θ = 1和诱导公式）。注意，半角公式有多种形式，这里给出的是其中一种常见的形式。

此外，cot函数还有一些和差公式和积和公式。和差公式允许我们通过两个角的三角函数值来计算它们的和或差的三角函数值。对于cot函数，我们有cot(α ± β) = (cotαcotβ - 1) ± cotα + cotβ / cotαcotβ + 1。这些公式在解决复杂的三角问题时非常有用。

积和公式则允许我们通过两个角的三角函数值的乘积来找到与它们相关的另一个角的三角函数值。然而，对于cot函数来说，直接的积和公式并不常见，但可以通过其他三角函数（如sin、cos或tan）的积和公式以及cot与这些函数的关系来推导。

在实际应用中，cot函数经常与其他三角函数一起使用，以解决各种几何和物理问题。例如，在光学中，cot函数可以用来描述光线的折射现象；在电气工程中，cot函数可以用于计算电感器的阻抗；在机械工程中，cot函数则可以帮助我们分析机构的运动和受力情况。

最后，需要注意的是，虽然cot函数在数学和物理学中具有广泛的应用，但在某些情况下，使用其他三角函数（如tan或sec）可能更为方便或直观。因此，在选择使用哪种三角函数时，我们需要根据问题的具体要求和背景知识来做出判断。

综上所述，cot函数是三角函数中的一个重要成员，它与其他三角函数有着密切的关系和广泛的应用。通过了解cot的公式、恒等式和变换公式，我们可以更好地理解和应用这个函数，从而解决各种复杂的数学和物理问题。同时，我们也需要注意到cot函数在不同象限的符号和性质，以确保在计算和推理过程中的准确性。