揭秘！平行四边形与梯形的面积及周长计算公式全解析

在数学的世界里，几何图形以其独特的魅力和广泛的应用性，始终吸引着无数学子与爱好者的目光。其中，平行四边形与梯形作为基本而重要的几何形状，不仅在日常生活中随处可见，更在几何学、工程学乃至计算机科学等领域发挥着举足轻重的作用。今天，就让我们一起深入探索这两个图形的奥秘，特别是它们令人着迷的面积和周长公式，相信这些知识点定能激发你对于几何之美的新一轮好奇与热爱。

平行四边形的魅力：从定义到公式的精彩演绎

平行四边形，这个听起来就充满对称和谐之美的名词，实际上是指两组对边分别平行且等长的四边形。它的形态多变，从正方形、矩形到菱形，都是平行四边形的特殊形式，每一种都拥有自己独特的美学价值和实际应用。

面积公式：揭秘几何空间的奥秘

平行四边形的面积计算，是几何学习中的一个重要里程碑。想象一下，你站在一个由平行四边形构成的花园里，想要知道这片绿地的面积以便种植花草，这时，面积公式就显得尤为重要了。平行四边形的面积等于底乘以高，简洁而有力。这里的“底”可以是任意一组对边中的一条，“高”则是从这条底边出发，垂直于底边并到达平行四边形另一侧的最短距离。通过这个公式，即便是最不规则的平行四边形，我们也能迅速准确地计算出它的面积，感受数学带来的便捷与美妙。

周长公式：勾勒图形的轮廓之美

如果说面积是平行四边形内在空间的度量，那么周长则是其外在边界的描绘。平行四边形的周长，即四条边的总和，计算公式同样直观明了：将两组对边的长度分别相加即可。这一公式不仅帮助我们了解平行四边形的大小规模，还引导我们关注其形状的比例与对称性。在艺术创作或建筑设计中，合理利用平行四边形的周长特性，可以创造出既美观又实用的结构布局。

梯形的智慧：从简单到复杂的优雅过渡

如果说平行四边形是几何世界的优雅舞者，那么梯形则更像是智慧的探索者，它在平行四边形的基础上，通过一条不平行的对角线，实现了从规则到不规则、从简单到复杂的优雅过渡。梯形只有一对对边平行，这一特性赋予了它更加多变和灵活的形态，也让我们在探索其面积和周长的过程中，体验到更多的乐趣与挑战。

面积公式：巧妙转化，智慧尽显

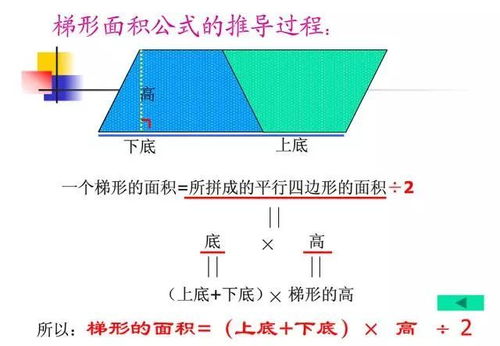
梯形的面积计算，相较于平行四边形，稍显复杂，却也更加富有挑战性。梯形面积的计算公式为（上底+下底）×高÷2，这里的“上底”和“下底”分别指梯形中较短的平行边和较长的平行边，“高”则是垂直于这两平行边且连接它们的线段。这个公式的背后，隐藏着一个巧妙的转化思维：我们可以将梯形想象成是由一个矩形和两个三角形组成，通过计算这三个部分的面积之和，再经过适当的调整，最终得到了梯形的面积公式。这一过程，不仅锻炼了我们的逻辑思维和解决问题的能力，也让我们深刻体会到几何学的智慧与魅力。

周长公式：边界的艺术，形态的多样

梯形的周长计算，虽然同样是将四条边的长度相加，但因其形态多变，使得这一计算过程充满了探索的乐趣。无论是等腰梯形（两腰等长）还是不等腰梯形，通过精确测量每条边的长度，我们都能得到其周长，进而对其整体形态有更直观的把握。在设计梯形结构的家具、桥梁或是装饰图案时，对周长的精确计算，是确保设计合理性和美观性的关键。

平行四边形与梯形的实际应用：从生活到科学的跨越

平行四边形与梯形不仅在几何学领域占据重要地位，它们的应用更是广泛而深远。在建筑设计中，利用平行四边形的稳定性和梯形的灵活性，可以创造出既坚固又富有美感的建筑结构；在平面设计领域，梯形元素的使用，能够打破传统对称布局的局限，为设计作品增添动感和层次感；在物理学中，平行四边形的力学特性和梯形的面积变化，为解决实际问题提供了科学依据；在计算机图形学中，平行四边形和梯形的算法优化，更是推动了图像处理、游戏开发等领域的快速发展。

结语：几何之美，探索不息

综上所述，平行四边形与梯形作为几何世界中的璀璨明珠，其面积和周长公式的探索与应用，不仅让我们领略到了数学的严谨与美丽，更激发了我们对于未知世界的好奇与探索欲。每一次公式的推导，每一次应用的实践，都是对智慧的一次挑战，对美的一次追求。在这个充满无限可能的世界里，让我们继续携手前行，在几何的海洋中遨游，共同探寻更多未知的奥秘，享受数学带来的乐趣与成就。