用几何画板创造神奇的毕达哥拉斯树：一步步操作指南

几何画板作为一款强大的数学绘图和教学辅助工具，不仅能够帮助用户直观地展示几何图形，还能通过动态演示揭示数学规律。在众多可绘制的图形中，毕达哥拉斯树无疑是一个兼具美学与数学意义的典范。毕达哥拉斯树，又称勾股树，是由一系列正方形和直角三角形构成的分形图案，其灵感来源于毕达哥拉斯定理（勾股定理）。下面，我们将详细介绍如何使用几何画板绘制毕达哥拉斯树的操作步骤，从准备工具、基本构造、细节优化到动态演示，全方位解析这一过程的每一个环节。

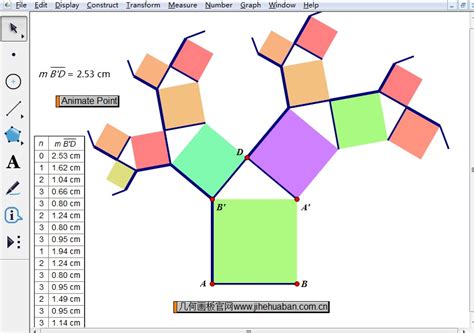
准备工具与环境

首先，确保你的计算机上已经安装了几何画板软件。几何画板有免费版本可供教育用途使用，以及更高级的专业版本。对于初学者来说，免费版本通常已经足够。安装完成后，打开几何画板，你将看到一个空白的绘图窗口和一些基本的绘图工具，如点工具、线段工具、圆工具等。此外，还可以使用“文本”工具添加注释，以及“度量”工具测量图形的属性。

基本构造原理

毕达哥拉斯树的构造基于勾股定理，即直角三角形的两条直角边的平方和等于斜边的平方（a² + b² = c²）。在绘制时，我们从一个正方形开始，然后在其内部构造一个直角三角形，该直角三角形的斜边与正方形的一边重合。接着，以直角三角形的两条直角边为边长，分别在正方形的两侧构造两个较小的正方形。这两个新正方形内又可以继续构造更小的直角三角形和正方形，如此往复，形成一棵不断分支的树状结构。

绘制第一个正方形

1. 选择点工具：在工具栏中点击点工具，然后在绘图窗口中任意位置点击，创建一个点作为正方形的左上角。

2. 构造线段：使用线段工具，依次连接这个点与另外两个点，形成一个正方形的三个边。为了保持正方形，可以使用“平行线”工具或“垂线”工具确保第四边与前三边平行且等长。

3. 完成正方形：通过调整点的位置或使用“度量”工具测量边长，确保正方形为规则的四边形。

构造直角三角形

1. 确定斜边：选择正方形的一条边作为直角三角形的斜边。

2. 构造中点：使用“中点”工具找到斜边的中点。

3. 绘制直角边：以中点为起点，使用线段工具构造两条分别与斜边垂直且相交于正方形边的线段，作为直角三角形的直角边。

4. 调整长度：根据勾股定理，确保两条直角边的平方和等于斜边的平方。可以通过“度量”工具验证这一点，或者直接利用几何画板的计算功能调整边长。

生成子正方形

1. 构造新正方形的顶点：以直角三角形的两个直角边为边长，分别在原正方形的两侧构造两个新的点，这两个点与正方形的顶点共同形成两个新的正方形。

2. 完成新正方形：使用线段工具连接这些点，形成两个较小的正方形。

递归构造毕达哥拉斯树

1. 选择模式：为了简化重复操作，可以使用几何画板的“递归”或“迭代”功能。然而，对于初学者来说，手动构造每个正方形和三角形可能更加直观，有助于理解构造过程。

2. 重复步骤：在每个新生成的正方形内，重复上述构造直角三角形的步骤，然后生成更小的正方形。每次重复时，都要确保新的直角三角形的斜边与原正方形的边平行或重合。

3. 调整布局：随着树的分支增加，你可能需要调整布局以避免图形重叠。可以使用“平移”工具或手动移动点来优化布局。

优化细节与美化图形

1. 颜色与填充：为了增强视觉效果，可以给不同的正方形和三角形分配不同的颜色或填充样式。使用“颜色”工具，选择你喜欢的颜色方案。

2. 隐藏辅助线：在构造过程中，可能会生成一些不必要的辅助线或点。使用“选择”工具选中这些元素，然后按键盘上的Delete键删除它们。

3. 添加标签：为了说明每个正方形的边长或三角形的边长比例，可以使用“文本”工具添加标签。标签内容可以包括边长数值、公式或注释。

4. 保存与导出：完成绘制后，不要忘记保存你的工作。几何画板支持多种文件格式，如.gsp（几何画板原生格式）、.png、.jpg等。你可以根据需要选择适当的格式导出图形。

动态演示与探索

1. 动画效果：几何画板允许你创建动画效果，以动态展示毕达哥拉斯树的生长过程。选择“动画”工具，设置动画的参数，如速度、循环次数等。

2. 动态测量：通过“度量”工具，可以实时测量图形的属性，如边长、角度等。在动画播放过程中，这些属性会动态更新，帮助你更直观地理解毕达哥拉斯树的数学特性。

3. 探索变化：你可以尝试改变初始正方形的边长、直角三角形的边长比例或分支的数量，观察这些变化对毕达哥拉斯树形状的影响。这不仅能加深你对勾股定理的理解，还能激发你对数学美的探索兴趣。

总结

使用几何画板绘制毕达哥拉斯树是一项既富有挑战性又充满乐趣的任务。它不仅考验你的绘图技能，还让你在实践中加深对勾股定理的理解。通过不断尝试和调整，你可以创造出独特而美丽的毕达哥拉斯树作品。这些作品不仅可以作为数学学习的辅助材料，还可以用于艺术创作或科学演示中。希望这篇指南能帮助你顺利掌握几何画板绘制毕达哥拉斯树的操作技巧，开启一段充满创意和探索的数学之旅。