轻松学会！几何画板中绘制勾股树的详细步骤

在探索数学的奇妙世界中，勾股定理无疑是一颗璀璨的明珠。它不仅揭示了直角三角形三边之间的基本关系，还为几何图形的创作提供了无限灵感。今天，我们将一起踏上一场数字与图形的创意之旅，通过“几何画板”这一强大的教育工具，学习如何绘制一幅既美观又富含数学哲理的勾股树。这不仅仅是一次绘图实践，更是一次对数学之美深度理解与欣赏的过程。

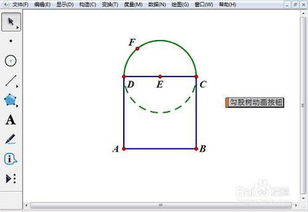
一、勾股定理的奇妙基础

勾股定理，即在一个直角三角形中，直角边的平方和等于斜边的平方（a² + b² = c²）。这个简洁而深刻的公式，自公元前6世纪由毕达哥拉斯学派发现以来，就成为连接代数与几何的桥梁。它不仅在数学领域有着广泛的应用，还在建筑、工程乃至天文学中发挥着不可替代的作用。

二、几何画板：创意的起点

“几何画板”是一款专为教育工作者和学生设计的动态几何软件，它能够帮助用户轻松创建、探索和展示几何图形及其性质。利用其强大的绘图功能和交互式界面，即便是复杂的几何图形也能被直观、生动地呈现出来。对于绘制勾股树这样的项目，几何画板无疑是一个理想的选择。

三、绘制前的准备

在开始绘制之前，确保你的电脑上已经安装了几何画板软件。打开软件后，一个空白的绘图窗口将出现在你面前，这里是创意绽放的舞台。为了方便操作，建议先熟悉一下界面上的基本工具，如点工具、直线工具、圆工具等，以及如何通过拖动和调整来改变图形的位置和大小。

四、构建基础直角三角形

1. 绘制直角边：使用直线工具，在画布上任意位置绘制两条垂直相交的线段，代表直角三角形的两条直角边。为了清晰起见，可以为这两条边赋予不同的颜色或标签（如a和b）。

2. 生成斜边：选择“构造”菜单下的“线段”选项，依次点击两条直角边的端点，软件将自动绘制出斜边c。此时，一个标准的直角三角形已经成形。

五、应用勾股定理验证

虽然这一步对于绘制勾股树不是必需的，但它能加深我们对定理的理解。利用几何画板的测量工具，分别测量三条边的长度，并在画布上显示这些测量值。你会发现，无论如何调整直角三角形的形状和大小，a² + b² 的值总是等于 c²，这正是勾股定理的直观体现。

六、绘制勾股树的分支

1. 确定生长点：选择直角三角形的斜边c作为勾股树的第一级分支的起点。在斜边上任取一点（非端点），这一点将成为新直角三角形的直角顶点。

2. 生成新直角三角形：从选取的点出发，分别向斜边的两端（或只向一端）作垂直线段，形成两个新的直角三角形。这些三角形的直角边分别是原斜边c的一部分，以及新添加的线段。

3. 递归构造：对每一个新生成的直角三角形，重复上述步骤，以其斜边为基础继续生成下一级分支。通过不断迭代，一个枝繁叶茂的勾股树逐渐成形。

七、调整与优化

在构建勾股树的过程中，几何画板允许你随时调整图形的各个参数，如改变直角三角形的比例、旋转角度或颜色等，以达到最佳视觉效果。尝试使用不同的颜色方案或添加渐变效果，可以使你的勾股树更加生动有趣。

八、探索数学之美

勾股树的绘制过程，不仅是一次技术实践，更是一次对数学之美的深度探索。每一级分支的生成，都是对勾股定理的一次应用，也是对自然界中递归现象的模拟。观察这棵树，你会发现它既有严格的数学逻辑支撑，又不失自然界的和谐与美感。

九、教育意义与启示

勾股树的绘制，不仅适合作为数学课堂上的一个教学案例，激发学生对几何学和代数的兴趣，也是培养学生逻辑思维、空间想象能力和创新思维的有效途径。通过这个项目，学生可以亲身体验到从理论到实践的转化过程，理解数学知识如何与现实世界相联系。

此外，勾股树的创作还启示我们，数学不仅仅是抽象符号和公式的堆砌，它蕴含着丰富的美学价值和创造潜力。在数学的世界里，每一个定理、每一个公式都可能是打开新世界大门的钥匙，引领我们发现未知、创造奇迹。

十、结语

随着勾股树在几何画板上的缓缓展开，我们不仅学会了一项实用的绘图技能，更重要的是，我们体验到了数学探索的乐趣和魅力。勾股树以其独特的形态，向我们展示了数学与艺术的完美融合，激发了我们对于知识无限可能的想象。在未来的学习和生活中，愿我们每个人都能像绘制勾股树一样，勇敢地探索未知，用智慧和创造力点亮前行的道路。

通过这次旅程，我们不难发现，数学不仅仅是书本上的知识，它更是连接现实与梦想的桥梁，是激发人类创造力和想象力的源泉。让我们带着这份对数学的热爱和敬畏，继续在知识的海洋中遨游，探索更多未知的美丽风景。