揭秘！圆柱侧面积的计算奥秘

圆柱的侧面积等于底圈周长与高的乘积。

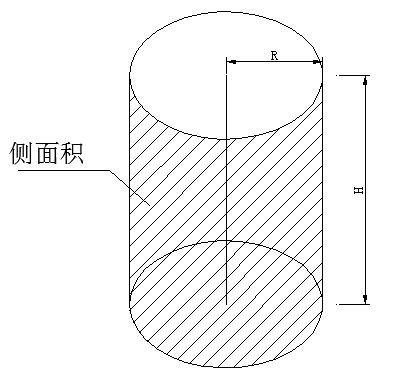
当我们深入探讨圆柱这一几何形状时，其侧面积的计算无疑是一个核心话题。圆柱作为日常生活中常见的立体图形，无论是水杯、罐头还是建筑中的某些结构，都频繁出现其身影。在这些实际应用中，了解如何准确计算圆柱的侧面积对于设计、制造以及材料估算等环节都至关重要。

首先，我们需要明确圆柱的基本结构。圆柱由一个矩形围绕其一边旋转一周形成，这个矩形的一边成为了圆柱的高，而另一边则形成了圆柱的底面圆的半径。由此，圆柱便拥有了两个完全相同的底面圆和一个侧面。

在圆柱的侧面积计算中，我们主要关注的是其侧面部分。侧面展开后，实际上就是一个矩形。这个矩形的长，就是圆柱底面的周长，也即圆的周长公式C=2πr（r为底面圆的半径）所表示的长度。而矩形的宽，则恰好等于圆柱的高h。

因此，圆柱的侧面积计算公式为：侧面积=底面周长×高=2πr×h。这个公式简单明了，却蕴含着几何与代数的巧妙结合。通过它，我们可以迅速准确地计算出任意圆柱的侧面积。

为了更好地理解和应用这个公式，我们可以举几个具体的例子。

假设我们有一个半径为3厘米、高为5厘米的圆柱。要计算其侧面积，我们只需将半径和高代入公式：侧面积=2π×3×5=30π平方厘米。如果我们需要一个更具体的数值，可以使用π的近似值3.14来进行计算：侧面积≈30×3.14=94.2平方厘米。

再来看一个更复杂的例子。假设我们有一个底面直径为10米、高为20米的圆柱。首先，我们需要将直径转换为半径，即半径r=直径/2=10/2=5米。然后，将半径和高代入公式计算侧面积：侧面积=2π×5×20=200π平方米。同样地，我们可以使用π的近似值3.14来得到一个具体的数值：侧面积≈200×3.14=628平方米。

在实际应用中，圆柱的侧面积计算有着广泛的应用场景。例如，在包装设计中，我们需要知道圆柱体的侧面积来确定包装材料的尺寸；在建筑工程中，圆柱体结构的侧面积对于涂料的用量、防水处理等都有着重要的参考价值；在机械制造中，了解圆柱体的侧面积可以帮助我们更准确地估算所需材料的数量。

此外，圆柱的侧面积计算还与一些其他几何问题紧密相连。例如，当我们需要将一个圆柱体切割成一个最大的长方体时，就需要利用圆柱的侧面积来求解长方体的最大可能面积；又比如，在解决一些涉及圆柱体滚动、滑动等动态问题时，圆柱的侧面积也会成为一个重要的考虑因素。

值得注意的是，虽然圆柱的侧面积计算相对简单，但在实际应用中仍需注意一些细节问题。例如，当圆柱体的底面不是完全水平的，或者圆柱体本身存在倾斜、扭曲等变形时，我们就不能直接使用上述公式进行计算。此时，我们需要根据具体情况进行适当的调整和修正。

此外，在计算过程中还需注意单位的一致性。例如，当半径和高以不同的单位给出时（如半径以厘米为单位，高以米为单位），我们需要先将其统一为相同的单位再进行计算。否则，计算结果将会出现错误。

总的来说，圆柱的侧面积等于底圈周长与高的乘积这一公式是几何学中一个重要的结论。它不仅具有理论上的意义，更在实际应用中发挥着巨大的作用。通过准确计算圆柱的侧面积，我们可以更好地理解和利用这一几何形状，为生活和工作带来更多的便利和效益。

在未来的学习和实践中，我们还将遇到更多与圆柱相关的几何问题。届时，我们可以利用圆柱的侧面积计算公式以及其他相关的几何知识来求解这些问题。同时，我们也可以通过不断的实践和创新来拓展圆柱的侧面积计算公式的应用范围和价值。

总之，圆柱的侧面积计算是几何学中的一个重要课题。通过深入学习和理解这一知识点，我们可以更好地掌握几何学的精髓和魅力，为未来的学习和工作打下坚实的基础。希望这篇文章能够帮助大家更好地理解圆柱的侧面积计算，并在实际应用中发挥出更大的作用。